MATEMATICAS IV
TEMARIO DE MATEMÁTICAS 4
domingo, 26 de mayo de 2013
BLOQUE 8
FUNCIONES PERIODICAS
FUNCIONES TRIGONOMÉTRICAS
FUNCIONES CIRCULARES
FORMAS SENOIDALES
REPRESENTACIÓN GRÁFICA DE FUNCIONES TRIGONOMÉTRICAS
CARACTERÍSTICAS DE LAS FUNCIONES PERIÓDICAS
Funciones Trigonometricas
Las funciones Trigonometricas son valores que varían con el tamaño de un ángulo. Un ángulo colocado en un plano semejante rectangular se dice que esta en la posición estándar si su vértice coincide con el origen y su lado inicial coincide con el eje positivo x.











donde: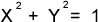 , luego:
, luego: 
El rango de estas funciones circulares es el conjunto de los números reales entre -1 y 1.
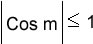 ...y...
...y...
Gráficas de las funciones circulares
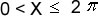
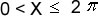

Una función se define entre un conjunto A y otro conjunto B en donde se establece una correspondencia entre los elementos de A con los elementos de B. Al conjunto A se le llama dominio de la función y B es el rango.
Para una función determinada, siempre hay una variable dependiente y otra variable independiente. La variable independiente representa los elementos del dominio y generalmente se grafica en el eje horizontal (X) y la variable dependiente se representará en el eje vertical (Y), entonces las representaremos en el sistema de coordenadas XY. Unas clases de funciones son:
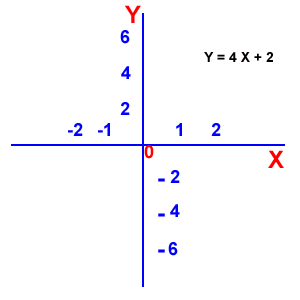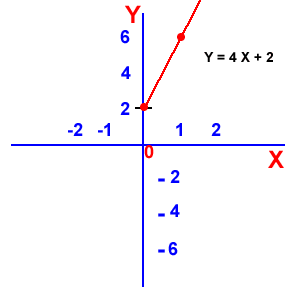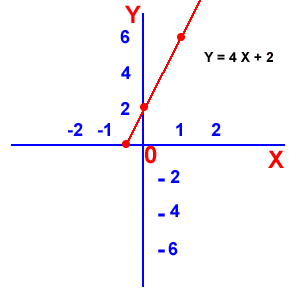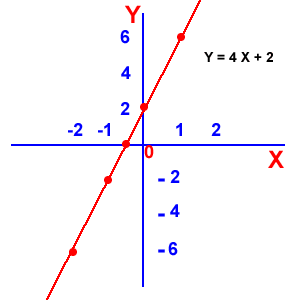
Función lineal: donde el dominio son los Reales, y el rango son los Reales.
 Función cuadrática: donde el dominio son los Reales y el rango son los Reales.
Función cuadrática: donde el dominio son los Reales y el rango son los Reales.
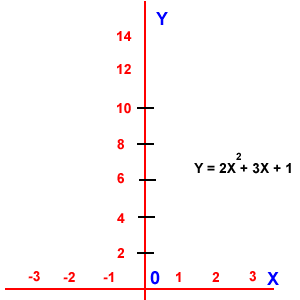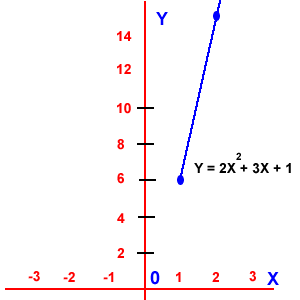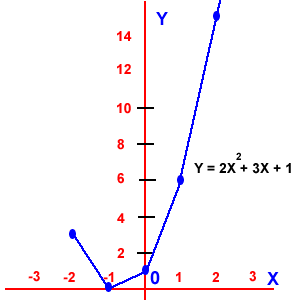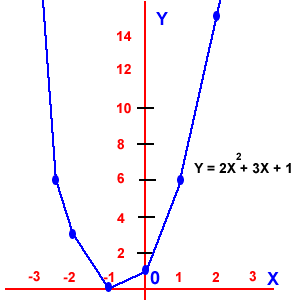 Función exponencial: El dominio son los números Reales y el rango son los números reales mayores que cero.(Y > 0).
Función exponencial: El dominio son los números Reales y el rango son los números reales mayores que cero.(Y > 0).
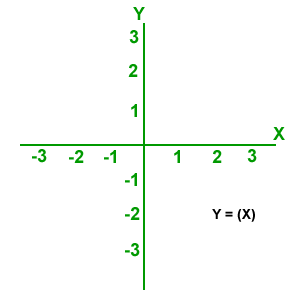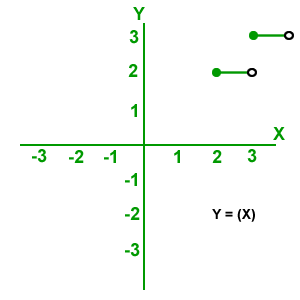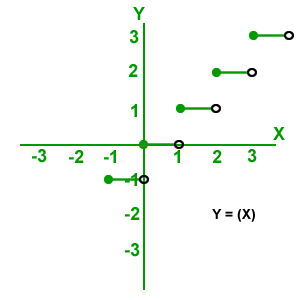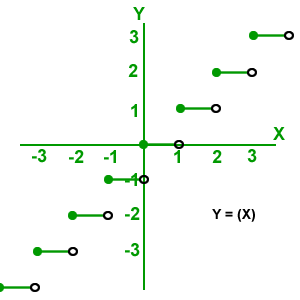
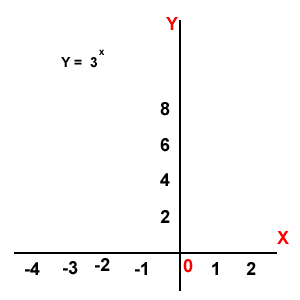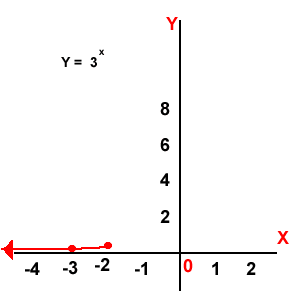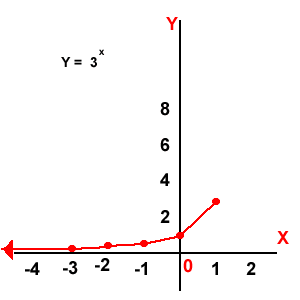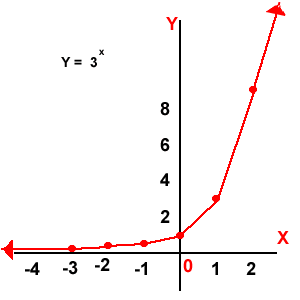 Función escalonada: (X): el mayor entero, cuyo valor sea menor o igual que X, el dominio son los números reales y el rango son los reales enteros.
Función escalonada: (X): el mayor entero, cuyo valor sea menor o igual que X, el dominio son los números reales y el rango son los reales enteros.
 También se definen funciones cuyos dominios son medidas de ángulos en posición normal en un sistema de coordenadas cartesianas XY.
También se definen funciones cuyos dominios son medidas de ángulos en posición normal en un sistema de coordenadas cartesianas XY.
Funciones Trigonométricas
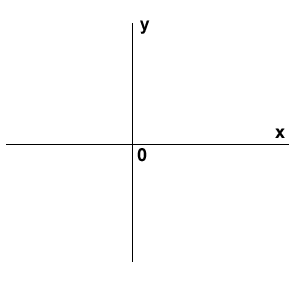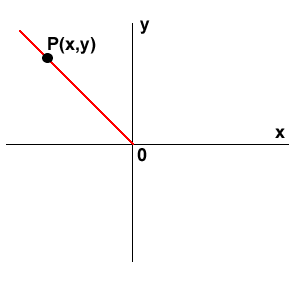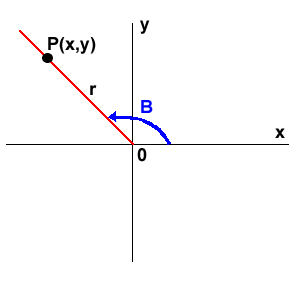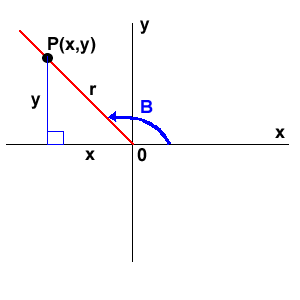
Sea un punto cualquiera P(x,y) (que no se encuentre en el origen) en el sistema de coordenadas cartesianas sobre la recta del lado final de un ángulo B en posición normal:
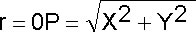 se defininen las funciones:
se defininen las funciones:
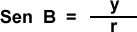 ,
, 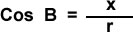 ,
,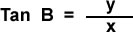
El dominio de las funciones seno y coseno es B: el ángulo en posición normal, y el rango esta entre -1 y 1, y el dominio de la función tangente es B: para todos los valores de x diferentes de cero y el rango son los números Reales.
FUNCIONES TRIGONOMÉTRICAS
FUNCIONES CIRCULARES
FORMAS SENOIDALES
REPRESENTACIÓN GRÁFICA DE FUNCIONES TRIGONOMÉTRICAS
CARACTERÍSTICAS DE LAS FUNCIONES PERIÓDICAS
Funciones Trigonometricas
Las funciones Trigonometricas son valores que varían con el tamaño de un ángulo. Un ángulo colocado en un plano semejante rectangular se dice que esta en la posición estándar si su vértice coincide con el origen y su lado inicial coincide con el eje positivo x.
En la Fig. 3, dejar a P (con coordenadas x y y ), ser cualquier punto a excepción del vértice sobre el lado terminal del ángulo q y r ser la distancia entre P y el origen. Cada una de las coordenadas x y y pueden ser positivas o negativas, dependiendo del cuadrante en que el punto P descansa; x puede ser cero, si P está sobre el eje y, o y puede ser cero, si P está sobre el eje x. La distancia r es necesariamente positiva y es igual al valor de », según el teorema Pitagórico.

Las funciones trigonométricas comúnmente usadas se definen como sigue:

Desde que x y y no cambian si 2p radianes se agregan al ángulo que es, 360° se agrega si es claro que el seno (q + 2p) = seno q. Las declaraciones similares se retienen para las otras cinco funciones. Por la definición, tres de estas funciones son reciprocas de los tres otros, que es,

Si el punto P, en la definición general de las funciones trigonométricas, está sobre el eje y, x es 0; por lo tanto, la división por cero es inadmisible en la matemáticas, la tangente y secante de tales ángulos como 90°, 270°, y -270° no existe. Si P está sobre el eje x, y es 0; en este caso, la cotangente y cosecante de tales ángulos como 0°, 180°, y - 180° no existen. Todos los ángulos tienen senos y cosenos, porque r nunca es igual a 0.
Desde que r es mayor o igual a x o y, los valores del seno q y coseno q se extienden desde - 1 a +1; la tangente q y cotangente q son ilimitadas, suponiendo cualquier valor verdadero; secante q y cosecante q puede ser igual o mayor de 1, o igual o menor que - 1.
Se muestra fácilmente que el valor de una función trigonometrica de un ángulo no depende de la elección particular del punto P, con tal que esté del lado terminal del ángulo, porque los radios solo dependen del tamaño del ángulo, no de donde el punto P se ubica sobre el lado del ángulo.
Si q es uno de los ángulos agudos de un triángulo derecho, las definiciones de las funciones trigonométricas dadas arriba pueden aplicarse a q como se indica a continuación (Fig. 4).
Imagine que el vértice A se pone en la intersección del eje x y el eje y en la Fig. 3, ese AC se extiende a lo largo del eje positivo x, y B es el punto P, para que AB = AP = r. Entonces el seno de q = y / r = un / c, y ese, como se indica a continuación:

los valores numéricos de las funciones trigonométricas de unos pocos ángulos pueden fácilmente obtenerse; por ejemplo, el ángulo agudo de un triángulo derecho isósceles es 45°, como se muestra en la Fig. 4. Por lo tanto, se indica que


Los valores numéricos de las funciones trigonométricas de cualquier ángulo pueden determinarse aproximadamente por sacar el ángulo en la posición estándar con una regla, brújula y transportador; por medir x, y, y r; y después por calcular las relaciones apropiadas. Realmente, es necesario que para calcular los valores del seno q y coseno q solo para unos ángulos seleccionados, porque los valores para otros ángulos y para las otras funciones pueden ser encontrados por usar una o más de las identidades trigonométricas que se enumeran más adelante.
Identidades Trigonométricas

Las fórmulas siguientes, llamadas identidades, que muestran las relaciones entre las funciones trigonométricas, retienen para todos los valores del ángulo q, o de dos ángulos, q y f, para que las funciones envueltas sean:

Por el uso repetido de una o más de las fórmulas en el grupo V, que es conocido como fórmulas de reducción, el seno q y el coseno q puede expresarse para cualquier valor de q, desde el punto de vista de los sinos y cosenos de ángulos entre 0° y 90°.
Por el uso de las fórmulas en los grupos I y II, los valores de la tangente q, cotangente q, secante q, y cosecante q puede encontrarse desde los valores del seno q y coseno q. Es por lo tanto suficiente para tabular los valores del seno q y coseno q para valores de q entre 0° y 90°; en práctica, para evitar cálculos tediosos, los valores de las otras cuatro funciones también se han hecho disponibles en tabulaciones para la misma gama de q.
La variación de los valores de las funciones trigonométricas para ángulos diferentes puede ser representada por diagramas, como en la Fig. 5. Se comprueba fácilmente desde estas curvas que cada de una de las funciones trigonométricas es periódica, que es, el valor de cada se repite en intervalos regulares llamados períodos. El período de todas las funciones, exceptúa la tangente y la cotangente, es 360°, o 2p radianes. La tangente y cotangente tiene un período de 180°, o p radianes. Muchas otras de las identidades trigonométricas pueden derivarse desde las identidades fundamentales. Todas se necesitan para las aplicaciones y estudio adicional de trigonometría.
a funciones trigonométricas asocian a cada número real, x, el valor de la razón trigonométrica del ángulo cuya medida en radianes es x.
Función seno
f(x) = sen x

Propiedades de la función seno
Dominio: 
Recorrido: [−1, 1]
Período: 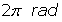
Continuidad: Continua en 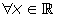
Creciente en: 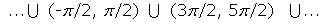
Decreciente en: 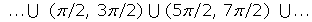
Máximos: 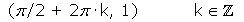
Mínimos: 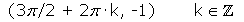
Impar: sen(−x) = −sen x
Cortes con el eje OX: 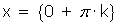
Función coseno
f(x) = cosen x

Propiedades de la función coseno
Dominio: 
Recorrido: [−1, 1]
Período: 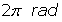
Continuidad: Continua en 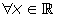
Creciente en: 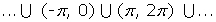
Decreciente en: 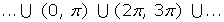
Máximos: 
Mínimos: 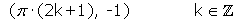
Par: cos(−x) = cos x
Cortes con el eje OX: 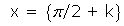
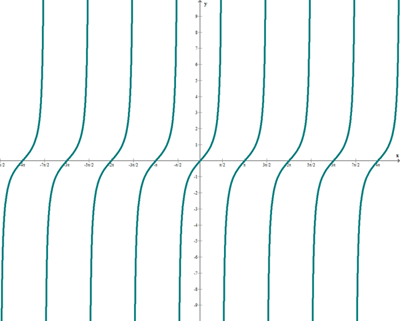
Función tangente
f(x) = tg x

Propiedades de la función tangente
Dominio: 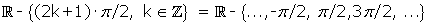
Recorrido: 
Continuidad: Continua en 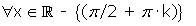
Período: 
Creciente en: 
Máximos: No tiene.
Mínimos: No tiene.
Impar: tg(−x) = −tg x
Cortes con el eje OX: 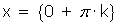
Función cotangente
f(x) = cotg x

Propiedades de la función cotangente
Dominio: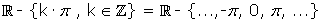
Recorrido: 
Continuidad: Continua en 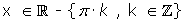
Período: 
Decreciente en: 
Máximos: No tiene.
Mínimos: No tiene.
Impar: cotg(−x) = −cotg x
Cortes con el eje OX: 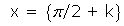
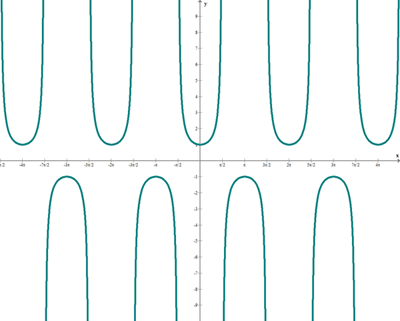
Función secante
f(x) = sec x

Propiedades de la función secante
Dominio: 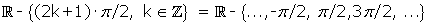
Recorrido: (− ∞, −1]  [1, ∞)
[1, ∞)
Período: 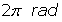
Continuidad: Continua en 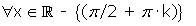
Creciente en: 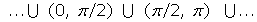
Decreciente en: 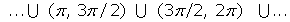
Máximos: 
Mínimos: 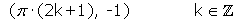
Par: sec(−x) = sec x
Cortes con el eje OX: No corta
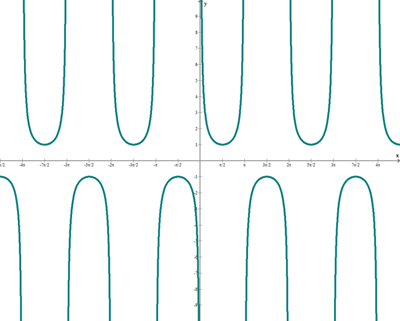
Función cosecante
f(x) = cosec x

Propiedades de la función cosecante
Dominio: 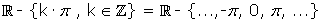
Recorrido: (− ∞, −1]  [1, ∞)
[1, ∞)
Período: 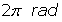
Continuidad: Continua en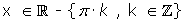
Creciente en: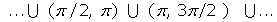
Decreciente en: 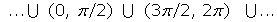
Máximos: 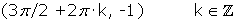
Mínimos: 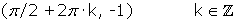
Impar: cosec(−x) = −cosec x
Cortes con el eje OX: No corta
Funciones Circulares
Los dominios de las funciones seno y coseno son el conjunto de los números reales, para un número real cualquiera m y V(m) = (x,y) se definen las funciones circulares seno y coseno:
Cos m = x , Sen m = y , V(m) = (x,y) = (Cos m, Sen m)donde:
El rango de estas funciones circulares es el conjunto de los números reales entre -1 y 1.
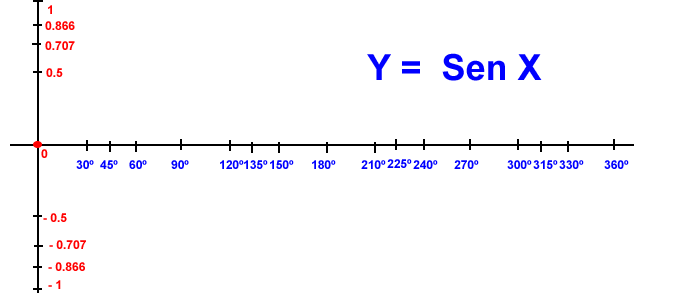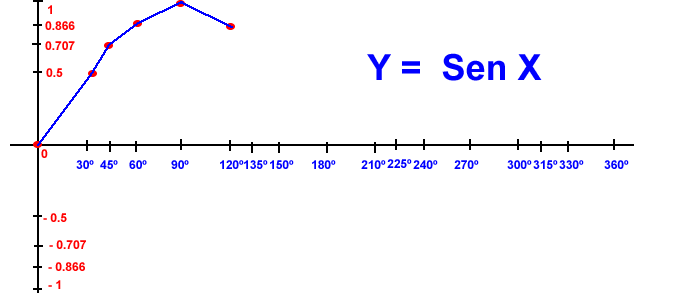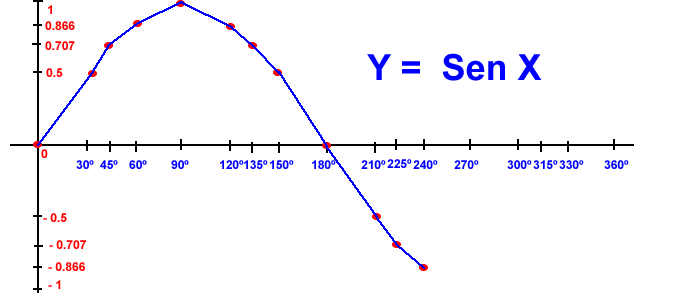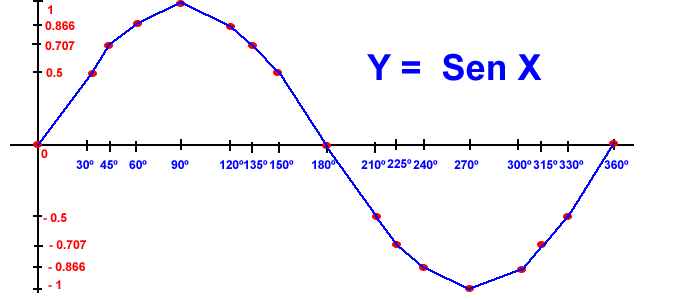
Gráficas de las funciones circulares
La gráfica g(m) = Sen m abarca todos los puntos de coordenadas ( m, sen m), ahora, si los referenciamos al sistema de coordenadas XY, tenemos que m se sustituye por Xy Sen m por Y para obtener la respectiva gráfica.
Podemos graficar la función dada para un intervalo dado, por ejemplo representaremos las funciones en el intervalo:
x
|
0
|
30º
|
45º
|
60º
|
90º
|
120º
|
135º
|
150º
|
180º
|
210º
|
225º
|
240º
|
270º
|
300º
|
315º
|
330º
|
360
|
0
|
0.5
|
0.70
|
0.86
|
1
|
0.86
|
0.70
|
0.5
|
0
|
-0.5
|
-0.70
|
-0.86
|
-1
|
-0.86
|
-0.70
|
-0.5
|
0
|

x
|
0
|
30º
|
45º
|
60º
|
90º
|
120º
|
135º
|
150º
|
180º
|
210º
|
225º
|
240º
|
270º
|
300º
|
315º
|
330º
|
360
|
1
|
0.86
|
0.70
|
0.70
|
0
|
- 0.5
|
0.70
|
-0.86
|
-1
|
-0.86
|
-0.70
|
-0.5
|
0
|
0.5
|
0.70
|
0.86
|
1
|

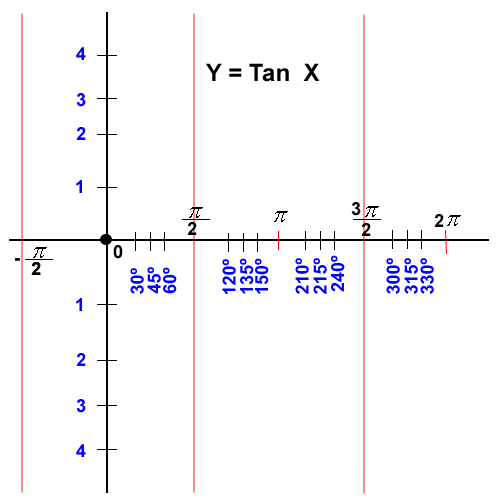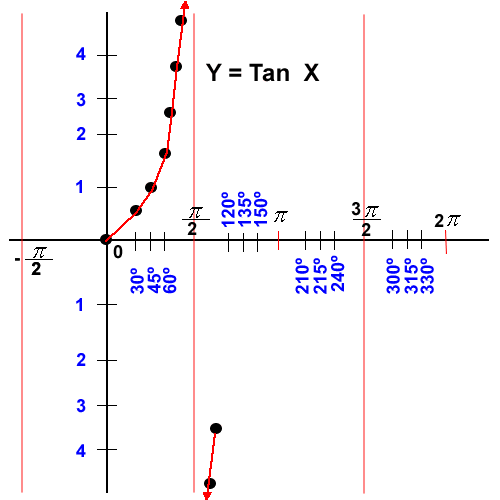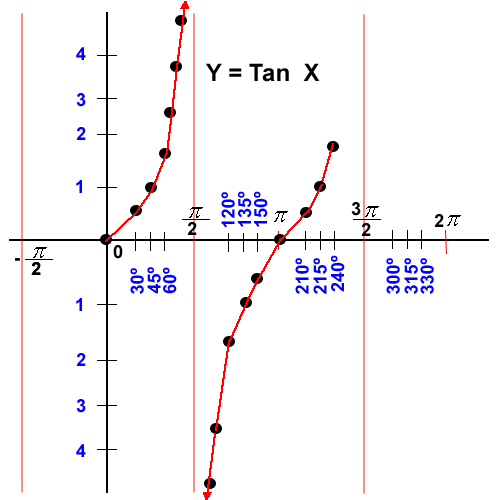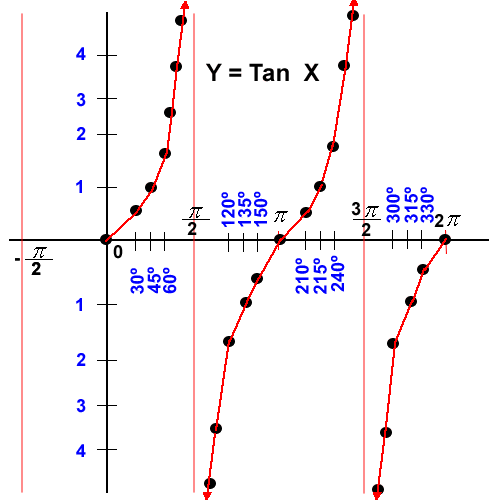
El rango de la función Y = Tan X es el conjunto de los números reales, no tiene valores máximos y mínimos y su amplitud es indefinida, la función en los puntos de 90º y 270º (y sus múltiplos) no es continua, es asíntota, es decir se aproxima a este valor pero sin tocarlo.
x
|
0
|
30º
|
45º
|
60º
|
90º
|
120º
|
135º
|
150º
|
180º
|
210º
|
225º
|
240º
|
270º
|
300º
|
315º
|
330º
|
360
|
0
|
0577
|
1
|
1.732
|
**
|
-1.732
|
- 1
|
-0.866
|
0
|
0.577
|
1
|
1.732
|
**
|
-1.732
|
- 1
|
-0.577
|
0
|

Una función se define entre un conjunto A y otro conjunto B en donde se establece una correspondencia entre los elementos de A con los elementos de B. Al conjunto A se le llama dominio de la función y B es el rango.
Para una función determinada, siempre hay una variable dependiente y otra variable independiente. La variable independiente representa los elementos del dominio y generalmente se grafica en el eje horizontal (X) y la variable dependiente se representará en el eje vertical (Y), entonces las representaremos en el sistema de coordenadas XY. Unas clases de funciones son:
Función lineal: donde el dominio son los Reales, y el rango son los Reales.
 Función cuadrática: donde el dominio son los Reales y el rango son los Reales.
Función cuadrática: donde el dominio son los Reales y el rango son los Reales.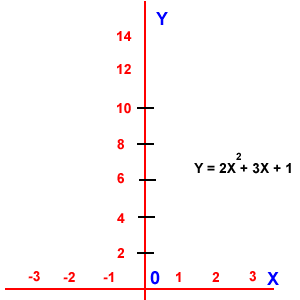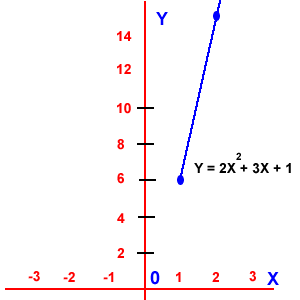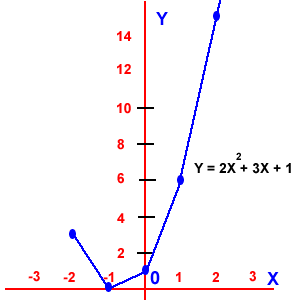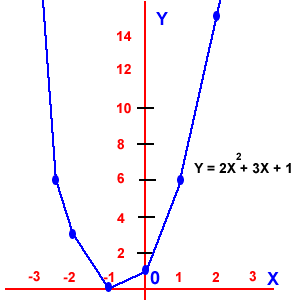 Función exponencial: El dominio son los números Reales y el rango son los números reales mayores que cero.(Y > 0).
Función exponencial: El dominio son los números Reales y el rango son los números reales mayores que cero.(Y > 0).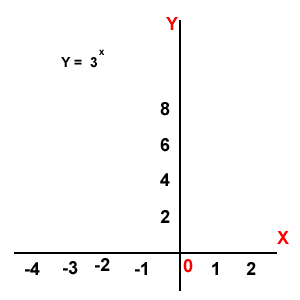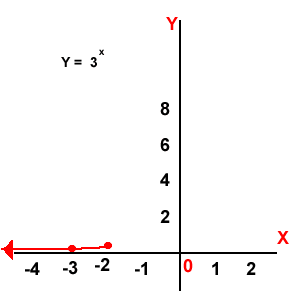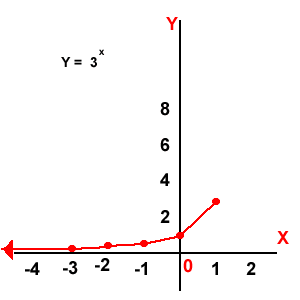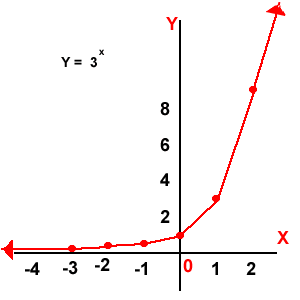 Función escalonada: (X): el mayor entero, cuyo valor sea menor o igual que X, el dominio son los números reales y el rango son los reales enteros.
Función escalonada: (X): el mayor entero, cuyo valor sea menor o igual que X, el dominio son los números reales y el rango son los reales enteros. También se definen funciones cuyos dominios son medidas de ángulos en posición normal en un sistema de coordenadas cartesianas XY.
También se definen funciones cuyos dominios son medidas de ángulos en posición normal en un sistema de coordenadas cartesianas XY.Funciones Trigonométricas
Sea un punto cualquiera P(x,y) (que no se encuentre en el origen) en el sistema de coordenadas cartesianas sobre la recta del lado final de un ángulo B en posición normal:

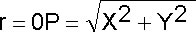 se defininen las funciones:
se defininen las funciones: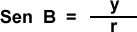 ,
, 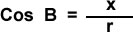 ,
,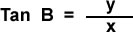
El dominio de las funciones seno y coseno es B: el ángulo en posición normal, y el rango esta entre -1 y 1, y el dominio de la función tangente es B: para todos los valores de x diferentes de cero y el rango son los números Reales.
Suscribirse a:
Entradas (Atom)