FUNCIÓN EXPONENCIAL
FUNCIÓN LOGARÍTMICA
GRÁFICA DE LA FUNCIÓN EXPONENCIAL Y LOGARÍTMICA
PROPIEDADES DE LOS EXPONENTES
PROPIEDADES DE LOS LOGARITMOS
ECUACIÓN EXPONENCIAL
ECUACIÓN LOGARÍTMICA
La función exponencial, es conocida formalmente como la función real ex, donde es el número de Euler, aproximadamente 2.71828...; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=ex o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.
En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma
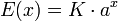
siendo a, K ∈ R números reales, con a > 0. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen.
La función exponencial ex puede ser definida de diversas maneras equivalentes entre sí, como una serie infinita. En particular puede ser definida como una serie de potencias:
o como el límite de la sucesión:

En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma
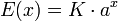
siendo a, K ∈ R números reales, con a > 0. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen.
La función exponencial ex puede ser definida de diversas maneras equivalentes entre sí, como una serie infinita. En particular puede ser definida como una serie de potencias:

o como el límite de la sucesión:

2.1.1 Teorema (Leyes de los Exponentes)
Sean a y b reales positivos y x,yÎÂ ,entonces:
1.


2.

3.

4.

5.
 .
. 6 .

Cuando a > 1 ,si x < y, entonces,
 .Es decir, cuando la base a es mayor que 1,la función exponencial
.Es decir, cuando la base a es mayor que 1,la función exponencial de base a es estrictamente creciente en su dominio.
Cuando 0 < a < 1, si x < y , entonces,
 .
. Esto significa que la función exponencial de base a < 1 es estrictamente decreciente en
su dominio.
 .
. 10.Si 0< a < b ,se tiene:

Esta propiedad permite comparar funciones exponenciales de diferentes bases.
11. Cualquiera que sea el número real positivo

 ,existe un único número real
,existe un único número real tal que
tal que  . Esta propiedad indica que la función exponencial es sobreyectiva.
. Esta propiedad indica que la función exponencial es sobreyectiva. Cuando x e y son enteros, los propiedades enunciadas anteriormente pueden demostrarse usando las definiciones y el teorema 1. Para el caso en el cual x e y son racionales, la demostración utiliza la definición y el teorema 2. Para el caso general, es decir, cuando x e yson reales, la demostración utiliza elementos del análisis real.
Gráfica de la Función Exponencial
En relación con las propiedades 7 y 8, enunciadas en el teorema, es conveniente hacer algunos comentarios adicionales.
En primer lugar, en las figuras 1 y 2, aparecen las gráficas de algunas funciones exponenciales de base a > 1 (fig. 1) y de base a < 1 (fig. 2).


Note que cuando la base a es mayor que 1,la función exponencial
 (fig.1) no está acotada superiormente. Es decir ,
(fig.1) no está acotada superiormente. Es decir ,  crece sin límite al aumentar la variable x. Además, ésta función tiene al cero como extremo inferior. Esto es ,
crece sin límite al aumentar la variable x. Además, ésta función tiene al cero como extremo inferior. Esto es ,  tiende a cero(0), cuando x toma valores grandes pero negativos.
tiende a cero(0), cuando x toma valores grandes pero negativos. Igualmente, cuando la base a < 1, la función exponencial
 (fig.2) no está acotada superiormente, pero su comportamiento para valores grandes de x, en valor absoluto, es diferente. Así,
(fig.2) no está acotada superiormente, pero su comportamiento para valores grandes de x, en valor absoluto, es diferente. Así,  crece sin límite, al tomar x valores grandes, pero negativos y
crece sin límite, al tomar x valores grandes, pero negativos y  tiende a cero, cuando la variable x toma valores grandes positivos.
tiende a cero, cuando la variable x toma valores grandes positivos. El hecho de ser la función exponencial
 con a > 1, estrictamente creciente (estrictamente decreciente cuando 0 < a < 1), significa que la función exponencial es inyectiva en su dominio.Este hecho y la continuidad de la función son las condiciones que se exigen para garantizar la existencia de la función inversa ( función logarítmica), que se presentan en la próxima sección.
con a > 1, estrictamente creciente (estrictamente decreciente cuando 0 < a < 1), significa que la función exponencial es inyectiva en su dominio.Este hecho y la continuidad de la función son las condiciones que se exigen para garantizar la existencia de la función inversa ( función logarítmica), que se presentan en la próxima sección. En relación con la propiedad 9, en un sentido, se deduce fácilmente de la definición de función; y, en otro, del hecho de ser la función exponencial inyectiva.
Observación.
Cuando a = e ,donde e es el número irracional cuya representación decimal con sus primeras cifras decimales, es e = 2.7182818284….,la función exponencial
 ,se llama: función exponencial de base e y, frecuentemente, se denota por Exp( x ) =
,se llama: función exponencial de base e y, frecuentemente, se denota por Exp( x ) =  .
.
Las Funciones Hiperbólicas
En algunos problemas de Física e Ingeniería, se presentan ciertas combinaciones de las funciones
 y
y  que por su interés y características especiales merecen ser consideradas con algún tratamiento. Tales combinaciones reciben el nombre de funciones hiperbólicas.
que por su interés y características especiales merecen ser consideradas con algún tratamiento. Tales combinaciones reciben el nombre de funciones hiperbólicas. Aquí solamente, se definirán y presentarán algunas identidades básicas que las relacionan.
La función COSENO HIPERBÓLICO, denotada por coshx, se define:
 ,
, 
La función logarítmica en base a es la función inversa de la exponencial en base a.



una función se llama logarítmica cuando es de la forma y = log a x donde la base a es un número real y positivo pero distinto de 1, puesto que el resultado sería 0.
Entonces se dan dos casos:
Base mayor que la unidad (a > 1)

Comparación: Las 3 funciones (log 2 x, log 5 x, log 7 x) se unen en el punto (1,0) porque el log a 1 = 0, y el log a a = 1, con lo que coincide que la gráfica pasa por (1,0) y (a,1).
En la función logarítmica (cuando a > 1) cuanto mayor es la base del logaritmo, más cerca del eje X está.
Las funciones de la forma y = log a x cuando la base es mayor que la unidad (a > 1) tienen las siguientes características:
(tomando como ejemplo la función f (x) = log 5 x)
-Dominio: el dominio de la función son los reales positivos puesto que no existe el logaritmo de un número negativo. Dom (f) = R +

En este tramo la función es negativa porque al introducir la antiimagen de un número racional la imagen que da, es un número negativo, lo que no quiere decir que existan imágenes para números negativos en esta función, ya que es imposible. log -x "
-Recorrido: el recorrido de la función es toda la recta real
ya que se ve como la función llega de -" y continua hacia + ".
-Continuas y crecientes: la función es creciente en todo su dominio porque...
...x < x' ! f(x) " f(x'), y continua porque todos sus puntos tienen imagen, tienen límite, y el límite de un punto coincide con la imagen del punto.
-Simetría: la función no es ni simétrica impar (por no ser simétrica respecto del origen) ni tampoco par (por no ser simétrica respecto del eje de coordenadas

no es simétrica respecto del origen
no es simétrica respecto del eje de ordenadas
-Asintotas: Partiendo del Dominio de la función ( Dom(f) = R+ ),

no se ven números concretos candidatos a asíntota por lo que viendo la gráfica deducimos que
x = 0, es una asíntota vertical y al probarlo comprobamos que es cierto.
lim log 5 x = - "
x ! 0 +
lim log 5 x = + "
x ! 0 -
No tiene asíntotas horizontales porque el limite cuando la función tiende a infinito no es un número concreto, (a simple vista se aprecia) al igual que no tiene asíntotas oblicuas.
Base positiva y menor que la unidad (0 < a < 1)

x

1/8 -3
1/4 -2
1/2 -1
1 0
2 1
4 2
8 3


x

1/8 3
1/4 2
1/2 1
1 0
2 −1
4 −2
8 −3

De la definición de logaritmo podemos deducir:
No existe el logaritmo de un número con base negativa.

No existe el logaritmo de un número negativo.

No existe el logaritmo de cero.

El logaritmo de 1 es cero.

El logaritmo en base a de a es uno.

El logaritmo en base a de una potencia en base a es igual al exponente.

PROPIEDADES DE LOS LOGARITMOS
Dos números distintos tienen logaritmos distintos.
Si

El logaritmo de la base es 1
 , pues
, pues 
El logaritmo de 1 es 0, cualquiera que sea la base
 , pues
, pues 
El logaritmo de un producto es igual a la suma de los logaritmos de los factores

El logaritmo de un cociente es igual al logaritmo del numerador menos el logaritmo del denominador

El logaritmo de una potencia es igual al exponente por el logaritmo de la base de la potencia

El logaritmo de una raíz es igual al logaritmo del radicando dividido por el índice

Cambio de base: El logaritmo en base a de un número se puede obtener a partir de logaritmos en otra base

EJERCICIOS
Expresa los logaritmos decimales de los siguientes números en función de
log 2.
Los números son los siguientes:
4, 16,
 ,
, 
0.5; 0.25; 0.125; 0.0625
 ,
,  ,
,  ,
, 
Hay que expresar los números dados en función de 2.
Cuando no ponemos la base del logaritmo se entiende que es 10, o sea que se trata de logaritmo decimal.
a)
 (Propiedad 6) à
(Propiedad 6) à 
b)
 (Propiedad 6) à
(Propiedad 6) à 
c)
 (Propiedad 6) à
(Propiedad 6) à 
d)
 (Propiedad 6) à
(Propiedad 6) à 
Ecuación exponencial
Una ecuación exponencial es aquella ecuación en la que la incógnita aparece en el exponente.
Para resolver una ecuación exponencial vamos a tener en cuenta:
1
2
3 Las propiedades de las potencias.
a0 = 1 ·
a1 = a
am · a n = am+n
am : a n = am - n
(am)n = am · n
an · b n = (a · b) n
an : b n = (a : b) n
Resolver las ecuaciones exponenciales:








Para despejar una incógnita que está en el exponente de una potencia, se toman logaritmos cuya base es la base de la potencia.

Sistemas de ecuaciones exponenciales
Un sistema de ecuaciones exponenciales es aquel sistema en los que las incógnitas aparecen en losexponentes.
Métodos de resolución de sistemas de ecuaciones exponenciales
1. Igualar los esponentes si los dos miembros tienen potencias con la misma base.
Resolver el sistema de ecuaciones exponenciales:

2. Realizar un cambio de variable.
Resolver el sistema de ecuaciones exponenciales:



No hay comentarios:
Publicar un comentario