martes, 2 de abril de 2013

BLOQUE 5

FUNCIONES FACTORIZABLES EN LA RESOLUCIÓN DE PROBLEMAS
CEROS Y RAÍCES DE LA FUNCIÓN
TEOREMAS DEL FACTOR Y DEL RESIDUO
DIVISIÓN SINTÉTICA
TEOREMA FUNDAMENTAL DEL ÁLGEBRA
TEOREMA DE FACTORIZACION LINEAL
GRÁFICAS DE FUNCIONES POLINOMIALES FACTORIZABLES


Ceros y raíces de la función 


Llamamos ceros o raíces de una función f a los valores de x para los cuales se cumple que f(x)=0. Los ceros de una función son las abscisas de los puntos en los cuales su gráfica tiene contacto con el eje de las x.

Raíces
Las raíces ( o ceros) de la función cuadrática son aquellos valores de x para los cuales la expresión vale 0, es decir los valores de x tales que y = 0. Gráficamente corresponden a las abscisas de los puntos donde la parábola corta al eje x. Podemos ver a continuación que existen parábolas que cortan al eje x en:




Ejercicio 1:
función polinómica:


f(x) = 2x3 + 7x2 - 7x - 12


Y nos piden hallar los ceros. Los ceros o raíces de una función son las "x" para las cuales la "y" (ó f(x)) vale cero. Es decir: son los números a los cuales, si le aplicas la función, el resultado dá cero. Se pueden hallar "igualando a cero" la fórmula de la función, que es lo mismo que "reemplazar por cero" a la "y" o a f(x) de la fórmula:


2x3 + 7x2 - 7x - 12 = 0


Ejercicio 2:


f(x) = x2 + x - 12

Cuando lo igualamos a cero y lo resolvemos tenemos:

x2 + x - 12 = 0 Igualando a cero.
(x + 4)(x - 3) = 0 Factorizando.
x = - 4 Solución 1
x = 3 Solución 2




Puesto que x1 = - 4 y x2 = 3 son soluciones de f(x) entonces f( -4 )= 0 y f( 3 )= 0. Decimos entonces que x = - 4 y x = 3 son raíces del polinomio f(x)= x2 + x - 12




Las raíces de f(x) = x3 - 4 x2 + x + 6 son x = - 1, x = 2 y x = 3
Teoremas del factor y del residuo 



Algoritmo de la división. Para cada polinomio de grado mayor o igual a uno y para cada número , existe un polinomio único de un grado menor que el de y un número único R, tal que:


.
Al polinomio se le denomina cociente, en el divisor y R es el residuo.




Teorema del residuo. Si es el residuo de dividir el polinomio entre , entonces .


Demostración.
Como por el algoritmo de la división, se tiene que si , .
O sea, .


Ejemplo 1:
Hállese el residuo de dividir el polinomio entre .
se puede escribir como , por tanto .
.
.
O sea que el residuo es 2.




Teorema del factor. Si es un cero del polinomio , entonces es un factor de .


Demostración.
Si es un cero de , .
Pero por el algoritmo de la división .
Como , .
Por tanto, y .


Ejemplo 2:
Use el teorema del factor para probar que es un factor de .
, así .
.
Luego –1 es un cero de .
Así es un factor de .





División sintética


La división sintética es un procedimiento "abreviado" para determinar el cociente y el residuo que se obtiene al dividir un polinomio $P(x)$ de grado$n, \, \, \, n \geq 1$, por un polinomio de la forma $x-\alpha$, con $\alpha \in I \!\!R$, a partir de los coeficiente de $P(x)$ y el cero de $x-\alpha$.

El procedimiento que usaremos para realizar la división sintética de un polinomio $P(x)$, por un polinomio de la forma $x-\alpha$, lo ilustraremos a través de ejemplos.





Ejemplo: 



Sean $P(x)$ y $Q(x)$ polinomios tales que:
$P(x) = 4x^3+3x^2-5x+2; \, \, \, \, Q(x) = x-3$
Determine el cociente y el residuo que se obtiene al dividir $P(x)$ por $Q(x)$:
a) Usando el método estudiado anteriormente (División larga)
b) Usando división sintética


Solución:


a)
Por lo que al dividir $P(x)$ por $Q(x)$ se obtiene $4x^2+15x+40$ como cociente y 122 como residuo.


b) Usando división sintética, $P(x)$ se divide por $Q(x)$ de la siguiente manera:
Donde los números 4, 15 y 40 son los coeficientes del cociente y 122 el residuo de la división.
Observe que, según la parte (a) de este ejercicio, los números obtenidos en la tercera fila son los coeficientes del cociente y el residuo, como se muestra en el esquema anterior.
Los números representados en la primera fila son los coeficientes de $P(x)$(dividendo) y el cero de $x-3$ (divisor).
Los números representados en la segunda fila se obtienen de la siguiente forma:
12 es el producto de 4 y 3
45 es el producto de 15 y 3
120 es el producto de 40 y 3
Los números representados en la tercera fila se obtienen de la siguiente forma:
4 es el coeficiente de $x^3$ en $P(x)$
15 es la suma de 3 y 12
40 es la suma de -5 y 45
122 es la suma de 2 y 120



Ejemplo:


Sean $P(x)$ y $Q(x)$ polinomios tales que: $P(x) = -8x^3+x^4-16+2x; \, \, \, Q(x) = x-8$.
Usando división sintética, determine el cociente  y el residuo $R(x)$ que se obtiene al dividir $P(x)$ por $Q(x)$.

Solución:


Ordenando $P(x)$ en forma desendiente de acuerdo a su grado, se obtiene:
$P(x) = x^4-8x^3+0x^2+2x-16$, y realizando la división se tiene:
Los números 1, 0, 0 y 2 son coeficientes del cociente. Y el número 0 es el residuo.

Por lo que $C(x) = x^3+0x^2+2x-16$ o sea $C(x) = x^3+2$ y 

Nota: Observe que al realizar la división sintética, tanto los coeficientes del dividendo que son diferentes de cero, como los que son iguales a cero, debem escribirse.





Ejemplo:

Sean $P(x)$ y $Q(x)$ polinomios tales que: $P(x) = x^3+x$ y $Q(x) = x+4$
Usando división sintética determine el cociente $C(x)$ y $Q(x)$.

Solución:

Como $P(x) = x^3+0x^2+x+0$ y el cero $x+4$ es -4 tenemos que:
Por lo tanto el cociente que se obtiene, al dividir $P(x)$ por $Q(x)$ es $x^2-4x+17$ y el residuo es -68.





Ejercicio: 


Para cada par de polinomios $A(x)$ y $B(x)$ que se definen a continuación determine por división sintética el cociente y el residuo que se obtiene al dividir $A(x)$ por $B(x)$.

1.$A(x) = x^5-32; \, \, \, \, B(x) = x-2$
2.$A(x) = -7x^2+8x+5x^3+1; \, \, \, \, B(x) = x-3$
3.$A(x) = x^3+27; \, \, \, \, B(x) = x+3$
4.$A(x) = x^3-2-3x; \, \, \, \, B(x) = x+5$
5.$A(x) = x^4-x; \, \, \, \, B(x) = x+1$
6.$A(x) = 6-5x+4x^2; \, \, \, \, B(x) = x+2$





TEOREMA FUNDAMENTAL DEL ALGEBRA

El teorema fundamental del álgebra establece que un polinomio en una variable, no constante y con coeficientes complejos, tiene tantas raíces como indica su grado, contando las raíces con sus multiplicidades. En otras palabras, dado un polinomio complejo de grado 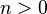, la ecuación tiene exactamente soluciones complejas, contando multiplicidades. De manera equivalente:
El cuerpo de los complejos es cerrado para las operaciones algebraicas.
Todo polinomio complejo de grado n se puede expresar como un producto de n polinomios de la forma .
El teorema se establece comúnmente de la siguiente manera:

Todo polinomio en una variable de grado n ≥ 1 con coeficientes reales o complejos tiene por lo menos una raíz (real o compleja).

Aunque ésta en principio parece ser una declaración más débil, implica fácilmente la forma completa por la división polinómica sucesiva por factores lineales.
El nombre del teorema es considerado ahora un error por muchos matemáticos, puesto que es más un teorema del análisis matemático que del álgebra.


TEOREMA DE FACTORIZACIÓN LINEAL.


Si f(x) es un polinomio de grado n, con n > 0, entonces f(x) tiene precisamente n
factoreslineales, es decir:
f(x) = a(x – c
1)(x – c
2)….(x – c
n),
en donde c
1, c
2,…..cn son números complejos y a es el coeficiente principal de f(x)











Publicado por en

3 comentarios:

  1. Unknown7 de mayo de 2014, 18:13

    genial, justo lo que necesito para mi resumen de matematicas

    ResponderEliminar
  2. Unknown19 de abril de 2016, 16:06

    Impresionante yo igual lo necesito para mi resumen todo eso lo voy a exponer gracias.....

    ResponderEliminar
  3. Anónimo21 de abril de 2018, 19:24

    gracias mi cuestionario esta completo

    ResponderEliminar

Suscribirse a: Enviar comentarios (Atom)