-FUNCIONES
-RELACIONES
-DOMINIO
-CONTRADOMINIO
-IMAGEN
-REGLA DE CORRESPONDENCIA
-FUNCIONES:
En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y(llamado codominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman el recorrido, también llamado rango).
-RELACIONES:
En matemática, Relación es la correspondencia de un primer conjunto, llamado Dominio, con un segundo conjunto, llamado codominio o Rango, de manera que a cada elemento del Dominio le corresponde uno o más elementos del codominio o Rango.
De las definiciones anteriores podemos deducir que todas las funciones son relaciones, pero no todas las relaciones son funciones.
También debemos agregar que toda ecuación es una Relación, pero no toda ecuación es una Función.
Todas las Relaciones pueden ser graficadas en el Plano Cartesiano
-DOMINIO:
Conjunto de todos los valores que toma la variable independiente, la x. Leemos de izquierda a derecha en el eje x y vemos para que valores hay función.
-CONTRADOMINIO:
El conjunto de todos los valores resultantes de la variable dependiente “y”. Otros nombres para éste son: recorrido ámbito ; imagen (muy utilizado en álgebra y teoría de conjuntos); y rango (muy empleado en cálculo).
Conjunto de todos los valores que toma la variable independiente, la x. Leemos de izquierda a derecha en el eje x y vemos para que valores hay función.
-CONTRADOMINIO:
El conjunto de todos los valores resultantes de la variable dependiente “y”. Otros nombres para éste son: recorrido ámbito ; imagen (muy utilizado en álgebra y teoría de conjuntos); y rango (muy empleado en cálculo).
-IMAGEN:
Se llaman imágenes a los elementos del conjunto de llegada o codominio que están asociados a una preimagen, mediante el criterio de la función.
REGLA DE CORRESPONDENCIA:
Una función es una correspondencia entre dos conjuntos A y B no vacíos, en la cual para todo elemento que pertenece al conjunto A existe un solo elemento, y solo uno, que pertenece al conjunto B al cual se le asocia o corresponde.
Para simbolizar que se ha establecido una función f, de un conjunto A en un conjunto B, se usa la siguiente notación:
f : A → B
EJEMPLOS DE FUNCIONES
Las funciones matemáticas pueden referirse a situaciones cotidianas, tales como: el costo de una llamada telefónica que depende de su duración, o el costo de enviar una encomienda que depende de su peso.
A modo de ejemplo, ¿cuál sería la regla que relaciona los números de la derecha con los de la izquierda en la siguiente lista?:
1 --------> 1
2 --------> 4
3 --------> 9
4 --------> 16
Los números de la derecha son los cuadrados de los de la izquierda.
La regla es entonces "elevar al cuadrado":
1 --------> 1
2 --------> 4
3 --------> 9
4 --------> 16
x --------> x2.
Para referirse a esta regla podemos usar un nombre, que por lo general es la letra f (de función). Entonces, f es la regla "elevar al cuadrado el número".
Usualmente se emplean dos notaciones:
x --------> x2 o f(x) = x2 .
Así, f(3) significa aplicar la regla f a 3. Al hacerlo resulta 32 = 9.
Entonces f(3) = 9. De igual modo f(2) = 4, f(4) = 16, f(a) = a2, etc.
Veamos algunos ejemplos que constituyen funciones matemáticas.
Ejemplo 1
Correspondencia entre las personas que trabajan en una oficina y su peso expresado en kilos
Conjunto X
|
Conjunto Y
|
Ángela
|
55
|
Pedro
|
88
|
Manuel
|
62
|
Adrián
|
88
|
Roberto
|
90
|
Cada persona (perteneciente al conjunto X o dominio) constituye lo que se llama la entrada o variable independiente. Cada peso (perteneciente al conjunto Y o codominio) constituye lo que se llama la salida o variable dependiente. Notemos que una misma persona no puede tener dos pesos distintos. Notemos también que es posible que dos personas diferentes tengan el mismo peso.
Ejemplo 2
Correspondencia entre el conjunto de los números reales (variable independiente) y el mismo conjunto (variable dependiente), definida por la regla "doble del número más 3".
x -------> 2x + 3 o bien f(x) = 2x + 3
Algunos pares de números que se corresponden por medio de esta regla son:
Conjunto X
|
Conjunto Y
|
Desarrollo
|
− 2
|
− 1
|
f(−2) = 2(−2) + 3 = −4 + 3 = − 1
|
− 1
|
1
|
f(−1) = 2(−1) + 3 = −2 + 3 = 1
|
0
|
3
|
f(0) = 2(0) + 3 = 0 + 3 = 3
|
1
|
5
|
f(1) = 2(1) + 3 = 2 + 3 = 5
|
2
|
7
|
f(2) = 2(2) + 3 = 4 + 3 = 7
|
3
|
9
|
f(3) = 2(3) + 3 = 6 + 3 = 9
|
4
|
11
|
f(4) = 2(4) + 3 = 8 + 3 = 11
|
Con estos ejemplos vamos entendiendo la noción de función: como vemos, todos y cada uno de los elementos del primer conjunto(X) están asociados a uno, y sólo a uno, del segundo conjunto (Y). Todos y cada uno significa que no puede quedar un elemento enX sin su correspondiente elemento en Y. A uno y sólo a uno significa que a un mismo elemento en X no le pueden corresponder dos elementos distintos en Y.
Ahora podemos enunciar una definición más formal:
Una función (f) es una regla que asigna a cada elemento x de un conjunto X (dominio) exactamente un elemento, llamado f(x), de un conjunto Y (codominio).
Otra definición equivalente es: sean X e Y dos conjuntos. Una función de X en Y es una regla (o un método) que asigna un (y sólo uno) elemento en Y a cada elemento en X.
Usualmente X e Y son conjuntos de números.
Generalizando, si se tiene una función f, definida de un conjunto A en un conjunto B, se anota
f : A -----> B (o, usando X por A e Y por B f : X -----> Y) o f(x) = x
Recordemos de nuevo que el primer conjunto A se conoce como dominio (Dom) de la función y B es el codominio o conjunto de llegada.
f(x) denota la imagen de x bajo f, mientras que x es la preimagen de f(x).
En el ejemplo 2 anterior el número 3 es la imagen del número 0 bajo f; por su parte, 1 es la preimagen del número 5.
El rango (Rg) o recorrido (Rec) o ámbito (A) es el conjunto de todos los valores posibles de f(x) que se obtienen cuando x varía en todo el dominio de la función.
Ejemplo 3
Suponga que el conjunto A (de salida) es A = {1, 2, 3} y que el conjunto B (de llegada) es B = {0, 4, 6, 8, 10, 12} y que la relación de dependencia o correspondencia entre A y B es "asignar a cada elemento su cuádruplo".
Vamos a examinar si esta relación es una función de A en B y determinaremos dominio y recorrido.
Veamos:
A los elementos 1, 2 y 3 del conjunto A les corresponden, respectivamente, los elementos 4, 8 y 12 del conjunto B. Como a cada elemento de A le corresponde un único elemento de Y, la relación de dependencia es una función (función de A en B).
Dominio = {1, 2, 3} Recorrido = {4, 8, 12}
Notar que el recorrido es un subconjunto del codominio B = {0, 4, 6, 8, 10, 12}
Aquí debemos recordar que toda función es una relación, pero no todas las relaciones son funciones. Como ejemplos de relaciones que son funciones y algunas que no lo son, veamos las siguientes:
Si tenemos los conjuntos
A = {1; 2; 3; 4}, B = {1; 2; 3; 4; 5}
Podemos establecer las relaciones
f = { (1; 2); (2; 3); (3; 4); (4; 5) }
g = { (1; 2); (1; 3); (2; 4); (3; 5); (4; 5) }
h = { (1; 1); (2; 2); (3; 3) }:
Está claro que f, g y h son relaciones de A en B, pero sólo f es una función (todos los elementos del conjunto A tiene su correspondiente elemento en b); g no es función ya que (1; 2) y (1; 3) repiten un elemento del dominio (el 1). Tampoco h es una función ya que Dom(h) = {1; 2; 3} ≠ A (falta el 4).
Ejemplo 4
Sea X = {−4, −1, 0, 4, 9}, Y = {−4,−3, −2, −1, 0, 1, 2, 3, 4} y que la regla de correspondencia es " asignar a cada elemento de X el resultado de extraer su raíz cuadrada".
Vamos a determinar si esta regla constituye función de X en Y.
Veamos:
A simple vista se aprecia que los números 0, 4, 9 tienen imagen en Y (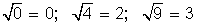
), pero a los números −4 y −1 no les corresponden elementos en Y. Como existen elementos de X que no se corresponden con elementos de Y, esta relación no es función de X en Y.
), pero a los números −4 y −1 no les corresponden elementos en Y. Como existen elementos de X que no se corresponden con elementos de Y, esta relación no es función de X en Y.Dominio y rango de una función
Como ya vimos, el dominio de una función es el conjunto de valores para los cuales la función está definida; es decir, son todos los valores que puede tomar la variable independiente (la x).
Por ejemplo la función f(x) = 3x2 – 5x está definida para todo número real (x puede ser cualquier número real). Así el dominio de esta función es el conjunto de todos los números reales.
En cambio, la función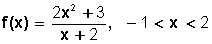
tiene como dominio todos los valores de x para los cuales −1< x < 2, porque aunque pueda tomar cualquier valor real diferente de –2, en su definición determina en qué intervalo está comprendida.
En cambio, la función
tiene como dominio todos los valores de x para los cuales −1< x < 2, porque aunque pueda tomar cualquier valor real diferente de –2, en su definición determina en qué intervalo está comprendida.
Si el dominio no se específica, debe entenderse que el dominio incluye a todos los números reales para los cuales la función tiene sentido.
En el caso de la función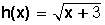 
, el dominio de esta función son todos los números reales mayores o iguales a –3, ya que x + 3 debe ser mayor o igual que cero para que exista la raíz cuadrada.
, el dominio de esta función son todos los números reales mayores o iguales a –3, ya que x + 3 debe ser mayor o igual que cero para que exista la raíz cuadrada.
Como resumen, para determinar el dominio de una función, debemos considerar lo siguiente:
Si la función tiene radicales de índice par, el dominio está conformado por todos los números reales para los cuales la cantidad subradical sea mayor o igual a cero.
Si la función es un polinomio; una función de la forma f(x) = a0 + a1x + a2x2 +...+ anxn (donde a0, a1, a2,..., an son constantes y nun entero no negativo), el dominio está conformado por el conjunto de todos los números reales.
Si la función es racional; esto es, si es el cociente de dos polinomios, el dominio está conformado por todos los números reales para los cuales el denominador sea diferente de cero.
El rango (recorrido o ámbito) es el conjunto formado por todas las imágenes; es decir, es el conjunto conformado por todos los valores que puede tomar la variable dependiente; estos valores están determinados además, por el dominio de la función.
Ejemplo
Identificar dominio y rango de la función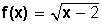 
Veamos:
Como la función tiene radicales el dominio está conformado por todos los valores para los cuales x – 2 ≥ 0. Esto es, el dominio de la función incluye todos los reales que son mayores o iguales a 2.
El rango es igual al conjunto de los números reales positivos incluyendo el cero; puesto que al reemplazar los valores del dominio se obtienen únicamente valores positivos bajo la función f.
En un sentido abstracto, calcular una función consiste en examinar la correspondencia general de “y” con respecto a “x”, expresado en la fórmula abstracta:
y = f(x)
Esta fórmula establece que la magnitud “y” está, de modo general, en función de “x”.
Ojo, que la magnitud “y” corresponde a lo que luego llamaremos “imagen”, y que depende del valor que se le asigne a “x” (que será la “preimagen”) en f(x).
La notación y = f (x) se lee “y” es una función de “x” o “y” es igual a f de x (esta notación no significa f por (x)). Obviamente en lugar de “x” e “y” hubiésemos podido emplear “variable”, y escribirlo así:
Variable dependiente = f (variable independiente)
Ejemplo 1
Si A = {1, 2, 3} y B = {2, 4, 6} y su correspondencia es el doble.
Entonces f(x) = 2x
En efecto
f(1) = 2 • 1 = 2
f(2) = 2 • 2 = 4
f(3) = 2 • 3 = 6
Tenemos
Dominio = {1, 2, 3}
Codominio = {2, 4, 6}
Ámbito (rango o recorrido) = {2, 4, 6}
Ejemplo 2
Si A = {1, 3, 5} y B = {3, 5, 7, 9, 11} y su correspondencia es el doble más uno.
Entonces f(x) = 2x + 1
En efecto:
f(1) = 2 • 1 + 1 = 3
f(3) = 2 • 3 + 1 = 7
f(5) = 2 • 5 + 1 = 11
Tenemos
Dominio = {1, 3, 5}
Codominio = {3, 5, 7, 9, 11}
Ámbito (rango o recorrido) = {3, 7, 11}
Conceptos básicos de la función
Dada una función f : A → B (es lo mismo que f : X → Y) se define:
* El conjunto A se llama conjunto de partida o dominio, se puede representar como f D.
* Al conjunto B se llama conjunto de llegada o codominio.
* Se llaman preimágenes a los elementos del conjunto de partida o dominio.
* Se llaman imágenes a los elementos del conjunto de llegada o codominio que están asociados a una preimagen, mediante el criterio de la función.
* Se llama rango (recorrido o ámbito) de una función al conjunto formado por las imágenes. Este conjunto es un subconjunto del codominio, se puede representar como f R ó f A, respectivamente.
Para ilustrar los conceptos anteriores usaremos lo que se denomina Diagramas de Venn-Euler.
Ejemplo 3
Analizar el siguiente diagrama que representa una función y determinar el dominio, codominio y el ámbito (rango o recorrido).
Tenemos
Dominio (Df) = {1, 2, 3, 4}
Codominio = {1, 4, 9, 16, 25}
Ámbito (Af) = {1, 4, 9, 16}
Ejemplo 4
Analizar el siguiente diagrama que representa una función y determinar el dominio, codominio y el ámbito.
Tenemos
Dominio (Df) = {1,2 3, 4}
Codominio = {−1, −2, −3, −4}
Ámbito (Af) = {−1, −2, −3, −4}
Recuerde que los elementos del dominio se llaman preimágenes y los
elementos del ámbito (rango o recorrido) se llaman imágenes.
Debido a que es posible que el codominio y el ámbito estén compuestos por el mismo conjunto de elementos, suele pensarse que codominio y ámbito es lo mismo, el concepto y los ejemplos anteriores nos permiten darnos cuenta que pensar así es un error.
Cálculo de la imagen
Debemos recordar que el conjunto de partida esta formado por las preimágenes y, se llama dominio, las preimágenes son los valores que toma la variable independiente.
Ejemplo 5
Un carpintero gasta $350 por cada silla que haga más un monto fijo de $2.000 por día ¿cuánto gastará si hace 2 sillas por día? ¿Cuánto gastará si hace 4, 6 u 8 sillas por día?
Para este ejemplo, x representa cada silla y f(x) el costo de fabricarla, lo cual significa que el costo es igual a multiplicar 350 por cada silla y sumarle el gasto fijo. Es decir:
f(x) = 350x + 2.000
Por lo que el valor de la variable independiente x para la primera pregunta es 2. Para encontrar la respuesta sustituimos el valor de dicha variable en el criterio de la función.
f(2) = 350 • 2 + 2.000
f(2) = 700 + 2.000
f(2) = 2.700
Entonces si hace solamente 2 sillas en un día, gastaría $2.700 en hacerlas.
De esto podemos decir que 2 es la preimagen de 2.700.
Además:
f(4) = 350 • 4 + 2.000 = 3.400
f(6) = 350 • 6 + 2.000 = 4.100
f(8) = 350 • 8 + 2.000 = 4.800
Tenemos, entonces:
fD = {2, 4, 6, 8}
Codominio: {2.700, 3.400, 4.100, 4.800}
Ejemplo 6
Tenemos f(x)= x2 – 6x +7 ¿Cuál es la imagen de 10?
Dado que nos preguntan por la imagen esto significa que 10 es una preimagen por lo que x = 10
f(10) = 102 − 6 • 10 + 7
f(10) = 100 − 60 + 7
f(10) = 47
Cálculo de la preimagen
Para calcular la preimagen de una función, conociendo la imagen y el criterio (el miembro de la derecha de la ecuación), se iguala el criterio de la función con la imagen que se tiene.
Despejando la incógnita de la ecuación que se forma se determina el valor de la variable.
Ejemplo 7
Si tenemos f(x)= x2 – 6 ¿Cuál es la preimagen de – 5 ?
Dado que nos preguntan por la preimagen esto significa que –5 es una imagen por lo que f(x) = –5
−5 = x2 – 6
− 5 + 6 = x2
1 = x2
x = ± 1
Las preimágenes de –5 son –1 y 1. Para este caso recordemos que en una función una imagen debe tener al menos una preimagen, aunque puede tener más de una.
Ejemplo 8
Si tenemos f(x)= 3x + 5 ¿Cuál es la preimagen de 11?
Dado que nos preguntan por la preimagen esto significa que 11 es una imagen por lo que f(x) = 11
11 = 3x + 5
11 − 5 = 3x
6 = 3x
2 = x
La preimagen de 11 es 2.
me podran ayudar en el problema de la pag 114 el insisio a
ResponderEliminarinsiso
ResponderEliminar